Newtonian Spacetime

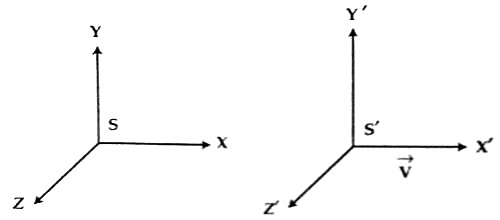
Newtonian Spacetime differs from Relativistic spacetime in that time is considered an absolute (i.e. t′=t). Transformations between reference frames can be achieved with Galilean transformations. A particle traveling along the x axis in S at a constant speed u, has a speed u′ found by:

u′x=dx′dt′=dx′dt=dxdt−v=ux−v

remembering that the first derivative of position is velocity, and the second derivative of motion is acceleration

[1] is derived from x′=x−vt of the Galilean transformations.