Newtonian Spacetime

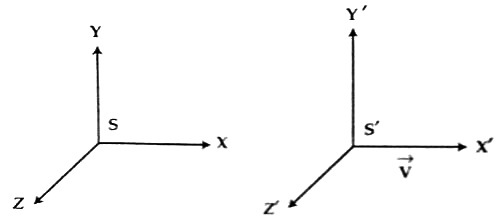
Newtonian Spacetime differs from Relativistic spacetime in that time is considered an absolute (i.e. $t^{\prime} = t$). Transformations between reference frames can be achieved with Galilean transformations. A particle traveling along the x axis in $S$ at a constant speed u, has a speed $u^{\prime}$ found by:

$$\begin{equation} u^{\prime}_{x} = \frac{dx^{\prime}}{dt^{\prime}} = \frac{dx^{\prime}}{dt} = \frac{dx}{dt} - v = u_{x} - v\tag{1} \end{equation}$$

remembering that the first derivative of position is velocity, and the second derivative of motion is acceleration

$[1]$ is derived from $x^{\prime} = x - vt$ of the Galilean transformations.