Inertial Frames

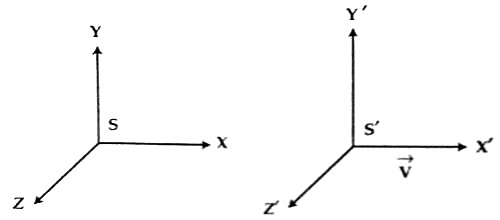
Above are two frames in Cartesian coordinates, S and S′. We have coordinates (x,y,z), which define our dimensions.

Inertial Frame #

An inertial frame is a frame of reference for which acceleration is zero. In other words:

d2xdt2=d2ydt2=d2zdt2=0

In the absence of gravity if S and S′ are two inertial frames they can only differ from each other by (and/or):

1. a translation
2. a rotation
3. a motion of one frame wrt the other under constant velocity