Inertial Frames

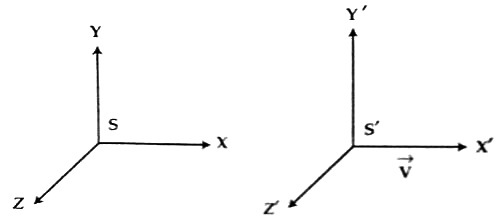
Above are two frames in Cartesian coordinates, $S$ and $S^{\prime}$. We have coordinates $(x, y, z)$, which define our dimensions.

Inertial Frame

An inertial frame is a frame of reference for which acceleration is zero. In other words:

$$\begin{equation} \frac{d^{2}x}{dt^{2}} = \frac{d^{2}y}{dt^{2}} = \frac{d^{2}z}{dt^{2}} = 0 \end{equation}$$

In the absence of gravity if $S$ and $S^{\prime}$ are two inertial frames they can only differ from each other by (and/or):

1. a translation
2. a rotation
3. a motion of one frame wrt the other under constant velocity