Gradient Descent

An optimization algorithm for finding the local minimum of a differentiable function.

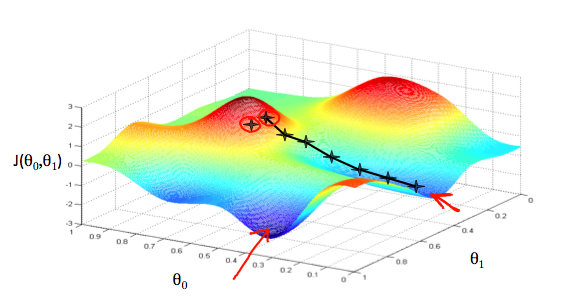
(The red arrows show the minimums of \(J(\Theta_{0},\Theta_{1})\), i.e. the cost function)

To find the minimum of the cost function, we take its derivative and “move along” the tangential line of steepest (negative) descent. Each “step” is determined by the coefficient \(\alpha\), which is called the Learning Rate.

\begin{equation} \Theta_{j_{new}} := \Theta_{j_{old}} - \alpha\frac{\partial}{\partial\Theta_{j}}J(\Theta_{0},\Theta_{1}) \end{equation}

\(\Theta_{j}\), initially, will be a randomly-chosen value. At each iteration of the algorithm, we want to update the “old” parameter \(\Theta_{j_{old}}\) with the newly-calculated value. This process should occur until the slope is zero (i.e. the derivative of the cost function is zero), indicating a minimum.