Injective Function

A function is injective (“one-to-one”) if

\(x \neq x^{\prime} \Longrightarrow f(x) \neq f(x^{\prime})\)

i.e. Given a set \(X\) and a set \(Y\), no two elements (say, \(x\) and \(x^{\prime}\)) from \(X\) map to the same element in \(Y\).

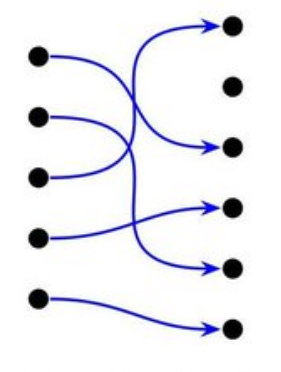
(Note: a function can be both injective and surjective, this image is injective only)